はじめに
この記事は、連載「ゼロから始める機械学習」 の4本目の記事となります。
前回「手動でのルールベース」 では、アヤメの分類タスクを設定し、手動でのルールベースによって解きました。
手動でのルールベースには、特徴量が多苦なると実装が現実的に不可能になるという課題がありました。
そこで機械学習の出番となるわけです。といっても、わかりやすくするために今回はタスクの内容は変えません。しかしながら、作成するプログラムは他のタスクにも応用が効く汎用的な内容になっていることに注意してください。
さて、最も基本的な機械学習モデルの一つであるロジスティック回帰について学びましょう。
ロジスティック回帰
ロジスティック回帰は、回帰ではなく分類タスクを解くためのモデルです。
ロジスティック回帰は厳密には二値分類のモデルですが、多値分類に拡張することができるため、ライブラリなどで(多値にも対応した)分類モデルとして実装されているでしょう。
二値分類とは
文字通りデータを二つのラベル(種類)に分類するタスクのことです。
二値と言っても、ラベルは数値である必要はありません。
アヤメの分類問題のように品種Aか品種Bかといったラベルで問題ありません。
ではなぜ二値分類と呼ばれるかというと、アルゴリズム上は0か1かを分類をするためです。つまり、プログラマがどちらの数字がどのラベルに対応するかを決めてあげれば良いのです。
数式
ロジスティック回帰は以下のような式で表されます。
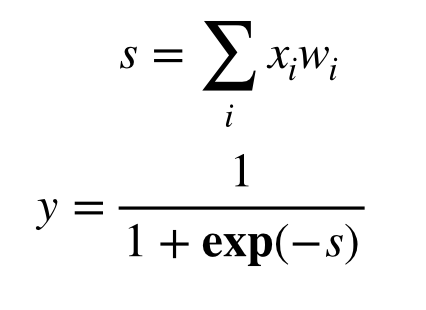
1 | x: 入力 |
まず、最初に理解していただきたいことは、ロジスティック回帰の出力yは0~1の間に収まるということです。これに対して適当な閾値(例えば0.5)を設けて、閾値以上であれば1と分類、そうでなければ0と分類したとみなします。
そして、wという変数が導入されています。
これが重みやパラメータと呼ばれる値で、学習によってより良いwを求めていくことになります。
より良いwとは
これが意外と難しい問いです。
少なくとも、完璧に分類ができるようなwは良いwと言えそうです。
そこで、正解率を指標にとっても良さそうですが、ここでは以下のような誤差関数を考え、
この誤差関数の値が小さいほど、良いwであると考えます。
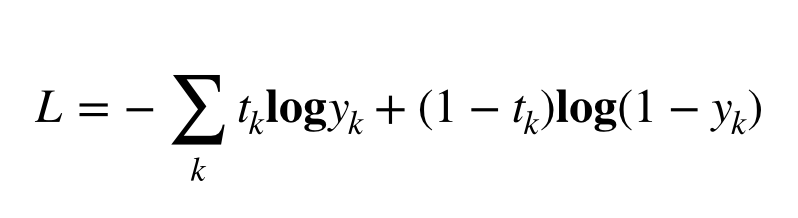
1 | L: 誤差関数 |
この関数はバイナリクロスエントロピーと呼ばれます。
なぜこの数式が出てくるかは省略しますが、最尤推定という考え方に基づいて導出が可能で、数学的なバックグラウンドがしっかりしていると考えていただければ良いです。
この数式は完璧な予測、すなわち
1 | t=y |
の時にL=0となり、それ以外ではL>0となります。
学習
では、具体的にwをどのように更新するのでしょうか。
勾配法という概念を用います。
勾配法では、誤差を減らすためにはwをどちらに動かせば良いかを考えます。
これはLをwで微分した値にマイナスを掛けることで得られます。
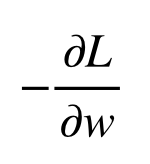
その値に学習率と呼ばれる係数を与えて、wを修正します。
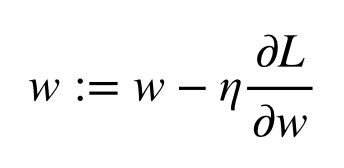
そして、修正は一度だけではなく何度も繰り返し行い、最終的n良いwを得ようとするのです。
実装
先にソースコードを載せます
1 | from sklearn.datasets import load_iris |
1 | class LogisticRegression: |
1 | lr = LogisticRegression() |
課題
評価方法に問題あり
さて、作成したプログラムは99%以上の精度を達成できたと思います。
しかし、このプログラムは実際のデータに対してそれだけの精度が出るでしょうか。
実は、そうとは限らないのです。
「機械学習とは?」 でも学んだように、
学習は既知のデータを扱うのに対し、予測では未知のデータを扱うことになります。
つまり、評価は未知のデータで行うべきです。
今回のプログラムでは、学習と評価を同じデータで行なっています。
なぜ同じデータを使ってはいけないのか
人間の勉強にたとえましょう。あなたがテストの作成者だとして、テスト前に問題を公表するでしょうか?
するべきではないでしょう。なぜなら、受験者が中身を理解せずに問題と答えを丸暗記してきてしまうからです。
機械学習の評価もこれと全く同じです。私たちはプログラムに丸暗記をして欲しいわけではないですよね。
ということで、次回は学習データとテストデータの分割について考えます。
記事情報
- 投稿日:2020年3月29日
- 最終更新日:2020年3月31日