Kaggle

短時間フーリエ変換(librosa.core.stft)

はじめに

Kaggle Free Sound Audio Tagging 2019で学ぶ音声処理ではKaggleコンペとその解法を題材に音声処理について解説しています。この記事は、スペクトログラムの計算に出てくるlibrosa.core.stftについて掘り下げます

librosa.core.stft

公式マニュアル

https://librosa.org/librosa/master/generated/librosa.core.stft.html

解説

通常、フーリエ変換は信号の全時間にわたって計算を行いますが、時間ごとに周波数に関する情報が欲しい場合は適しません。そういった場合に、短い区間に対するフーリエ変換を繰り返します。これが短時間フーリエ変換です。

パラメータ

  • y : np.ndarray [shape=(n,)], real-valued
  • n_fft : int > 0 [scalar]
  • hop_length : int > 0 [scalar]
  • win_length : int <= n_fft [scalar]
  • window : string, tuple, number, function, or np.ndarray [shape=(n_fft,)]
  • center : boolean
  • dtype : numeric type
  • pad_mode : string or function

win_lengthを変化させることにどのような意味があるのかを考察します。

準備

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import IPython.display as ipd
fname = 'input/0006ae4e.wav'
ipd.Audio(fname)
import librosa
y, sr = librosa.load('input/0006ae4e.wav')
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
def show_stft(n_fft,hop_length,win_length):
    S = np.abs(librosa.stft(y,n_fft,hop_length,win_length))**2
    melspec = librosa.feature.melspectrogram(S=S)
    log_melspec = librosa.power_to_db(melspec)
    librosa.display.specshow(librosa.power_to_db(S))
    plt.show()
    librosa.display.specshow(log_melspec)
    plt.show()

デフォルト値

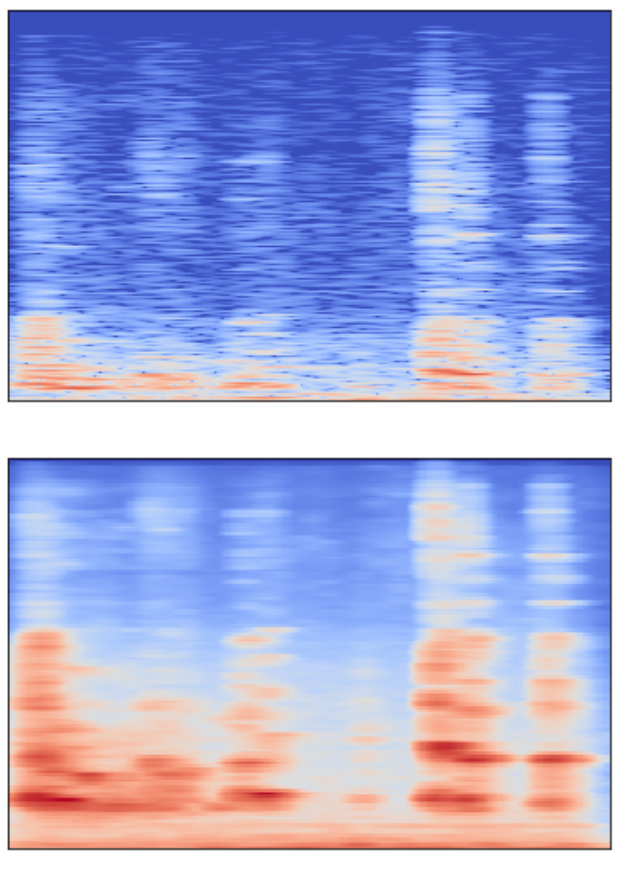
まずはデフォルト値から見てみます。デフォルトではwin_length=n_fftとなります。n_fftのデフォルト値は2048ですので、win_length=2048となります。

1
show_stft(2048,512,2048)

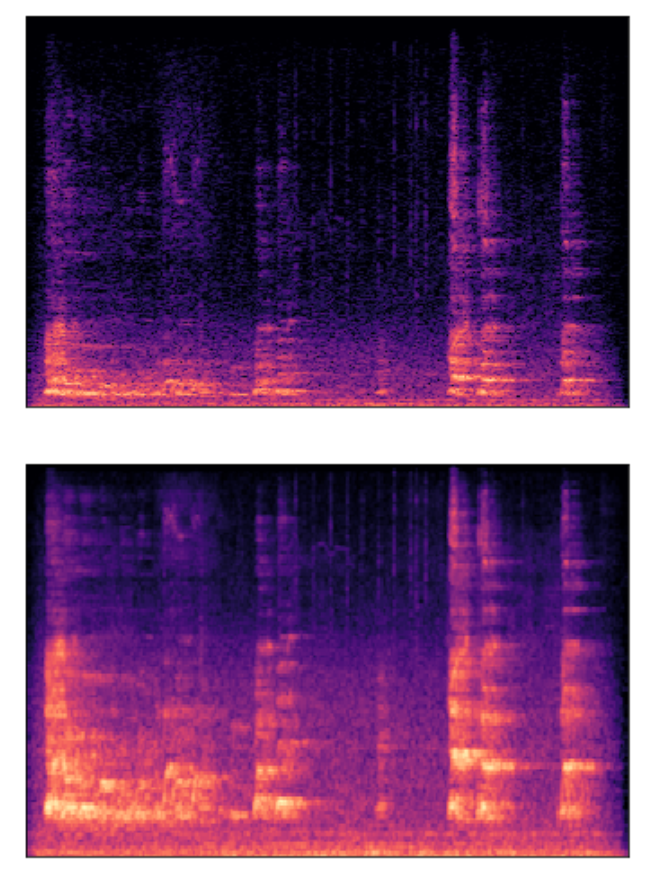
win_lenghtを小さくした場合

波形を小さく区切って周波数分析を行うと、時間分解能は細かくなるが、周波数分解能は粗くなる。

1
show_stft(2048,512,32)

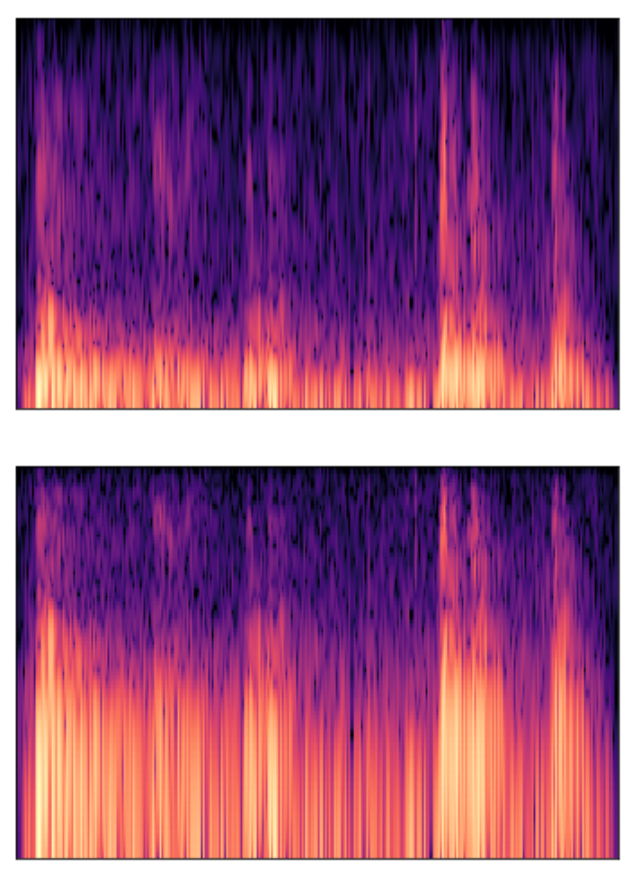
win_lenghtを大きくした場合

波形を大きく区切って周波数分析を行うと、周波数分解能は細かくなるが、時間分解能は粗くなる。

1
show_stft(16384,512,16384)

記事情報

  • 投稿日：2020年7月4日
  • 最終更新日：2020年7月4日